Logaritmo

► Los fundamentos de la teoría de los logaritmos

¿Cómo estaría hoy el conocimiento astronómico si el matemático y astrónomo alemán Johannes Kepler (1571–1630) hubiera tenido a su disposición una de esas modernas calculadoras electrónicas, tan comunes en nuestros días?

Esta cuestión provoca algunas reflexiones interesantes. Por ejemplo: el tiempo que Kepler gastaba en cálculos tediosos, como \( 3.25694 \cdot 1.78090 \) o \( 3.25694 : 1.78090 \), tan frecuentes en los estudios astronómicos, podría haber sido usado en investigaciones y, tal vez, ¡hoy tendríamos una cuarta ley de Kepler!

Hasta el siglo XVII, sin embargo, los cálculos con multiplicaciones o divisiones eran muy trabajosos, no solo en astronomía, sino en todas las ciencias que dependían de medidas. El escocés John Napier (1550–1617), también conocido como Neper, se preocupó seriamente por simplificar estos cálculos. Tras 20 años de investigación, publicó en 1614 el resultado de sus estudios: la teoría de los logaritmos.

El principio básico de los logaritmos es: transformar una multiplicación en una suma, y una división en una resta. Y como sumar o restar números es mucho más rápido que multiplicarlos o dividirlos…

La idea de Neper es relativamente simple: se representan los números positivos como potencias de un mismo número. Por ejemplo, cada columna de una tabla logarítmica muestra un número y su correspondiente representación como potencia de base 10. Así, en la primera entrada, tenemos: \( 1.78090 = 10^{0.2504} \).

▲ John Napier, creador de los logaritmos.

Resolución de sistema

Resolver:

\[ \left\lbrace \begin{array}{l} x = 2y – 3z \quad (1) \\ x + y + z = 6 \quad (2) \\ -2x + y – z = 5 \quad (3) \end{array} \right. \]

Sustituimos (1) en las ecuaciones (2) y (3):

En (2):
\[ 2y – 3z + y + z = 6 \Rightarrow 3y – 2z = 6 \quad (4) \]

En (3):
\[ -2(2y – 3z) + y – z = 5 \] \[ -4y + 6z + y – z = 5 \Rightarrow -3y + 5z = 5 \quad (5) \]

Nuevo sistema:

\[ \left\lbrace \begin{array}{l} 3y – 2z = 6 \quad (4) \\ -3y + 5z = 5 \quad (5) \end{array} \right. \]

Estudio completo

b) Estudio completo:

📌 Monotonía:
\[ f'(x) = \frac{3(x^2 + 10x + 15)}{(x + 5)^2} = 0 \Longrightarrow x = -5 + \sqrt{10}, \quad x = -5 – \sqrt{10} \]

\((-\infty, -5 – \sqrt{10})\)	\((-5 – \sqrt{10}, -5 + \sqrt{10})\)	\((-5 + \sqrt{10}, \infty)\)
+	−	+
\(f'(x)\)	\(f'(x)\)	\(f'(x)\)
creciente	decreciente	creciente

Luego la función tiene un Máximo en el punto \((-8{,}16;\ -43{,}97)\) y un Mínimo en el punto \((-1{,}84;\ -6{,}03)\).

📌 Curvatura:
\[ f”(x) = \frac{60}{(x + 5)^3} \neq 0 \quad \text{Luego la función no tiene puntos de Inflexión.} \]

\((-\infty,\ -5)\)	\((-5,\ \infty)\)
−	+
\(f”(x)\)	\(f”(x)\)
convexa \( \cap \)	cóncava \( \cup \)

Regla del Producto – Derivadas

🔹 Regla del Producto para Derivadas

Cuando una función está definida como el producto de dos funciones derivables, por ejemplo:

\( h(x) = f(x) \cdot g(x) \)

No podemos derivar término a término. En su lugar, usamos la regla del producto:

Teorema (Regla del producto):

Si \( f \) y \( g \) son funciones derivables en un punto \( a \), entonces:

\[ (f \cdot g)'(a) = f'(a) \cdot g(a) + f(a) \cdot g'(a) \]

Demostración

Sea \( h(x) = f(x) \cdot g(x) \). Aplicamos la definición de derivada:

\[ h'(a) = \lim_{x \to a} \frac{f(x)g(x) – f(a)g(a)}{x – a} \]

Sumamos y restamos \( f(a)g(x) \) en el numerador:

\[ = \lim_{x \to a} \frac{f(x)g(x) – f(a)g(x) + f(a)g(x) – f(a)g(a)}{x – a} \]

Agrupamos y factorizamos:

\[ = \lim_{x \to a} \left[ \frac{f(x) – f(a)}{x – a} \cdot g(x) + f(a) \cdot \frac{g(x) – g(a)}{x – a} \right] \]

Aplicando la definición de derivada:

\[ = f'(a) \cdot g(a) + f(a) \cdot g'(a) \]

Ejemplo aplicado

Calculemos la derivada de la función:

\( h(x) = x \cdot e^x \)

Aplicamos la regla del producto:

\[ h'(x) = (x)’ \cdot e^x + x \cdot (e^x)’ = 1 \cdot e^x + x \cdot e^x \]

Factorizando:

\[ h'(x) = e^x (1 + x) \]

Por lo tanto, la derivada de \( h(x) = x \cdot e^x \) es \( h'(x) = e^x (1 + x) \).

Ejercicio R4 – Sistemas Lineales

R4. Clasifica cada sistema de ecuaciones lineales como SPD, SPI o SI.

a) \[ \left\{ \begin{array}{l} 2x – y = -1 \\ x + y = 4 \end{array} \right. \]

Resolución

a) Usando el método de sustitución, aislamos \( y \) en la primera ecuación y sustituimos en la segunda:

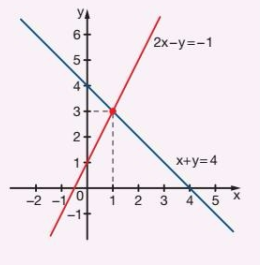
\( 2x – y = -1 \Rightarrow -y = -2x -1 \Rightarrow y = 2x + 1 \)
\( x + y = 4 \Rightarrow x + (2x + 1) = 4 \Rightarrow 3x + 1 = 4 \Rightarrow x = 1 \)
Sustituyendo \( x = 1 \) en \( x + y = 4 \Rightarrow y = 3 \)

Las rectas se cruzan en el punto (1,3), es decir, tienen una única solución.
Por lo tanto, el sistema es compatible y determinado (SPD).

b) \[ \left\{ \begin{array}{l} -x + y = 2 \\ 2x – 2y = 4 \end{array} \right. \]

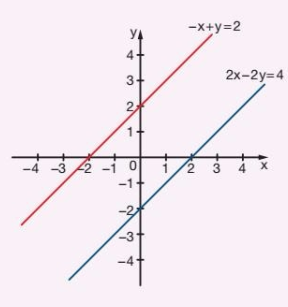
b) Usando el método de adición:

Multiplicamos la primera por 2: \( -2x + 2y = 4 \)
Sumamos con la segunda: \( 2x – 2y = 4 \)
\( 0x + 0y = 8 \): una ecuación imposible

La ecuación \( 0x + 0y = 8 \) no tiene solución en los números reales. Las rectas son paralelas, no tienen ningún punto en común.
Por lo tanto, el sistema es incompatible (SI).

Sistemas lineales equivalentes

Cuando dos sistemas lineales presentan las mismas soluciones, decimos que son equivalentes.

Los sistemas

\[ \begin{array}{l} \left\{ \begin{array}{rcl} 2x – y + 4z &=& 3 \\ -x – 3y – 2z &=& 6 \\ 3x – y + 5z &=& 4 \end{array} \right. \quad y \quad \left\{ \begin{array}{rcl} 3x + 2y – 2z &=& -1 \\ x + 2y – z &=& 3 \\ -3y + 5z &=& 1 \end{array} \right. \end{array} \]

son equivalentes porque ambos admiten como única solución la terna \( (-1, 3, 2) \).

En cambio, los sistemas

\[ \begin{array}{l} \left\{ \begin{array}{rcl} 2x – y + z &=& -2 \\ 5x + 2y – z &=& 3 \\ x + y + 4z &=& -5 \end{array} \right. \quad y \quad \left\{ \begin{array}{rcl} x + y + 2z &=& 6 \\ y – z &=& -1 \end{array} \right. \end{array} \]

no son equivalentes, ya que sus soluciones únicas son distintas: \( (0, 1, -1) \) y \( (2, 2, -3) \), respectivamente.

Propiedades de los sistemas equivalentes

Si multiplicamos una ecuación de un sistema \( S_1 \) por una constante real \( k \neq 0 \), obtenemos un sistema equivalente \( S_2 \).

Ejemplo:
Multiplicamos por 3 la primera ecuación del sistema \( S_1 \): \[ \left\{ \begin{array}{rcl} 2x + 3y – 4z &=& -6 \\ -3x + y + z &=& -7 \\ 5x – 2y + 9z &=& 23 \end{array} \right. \Rightarrow \left\{ \begin{array}{rcl} 6x + 9y – 12z &=& -18 \\ -3x + y + z &=& -7 \\ 5x – 2y + 9z &=& 23 \end{array} \right. \]

El sistema resultante es equivalente a \( S_1 \), y ambos tienen como única solución la terna \( (2, -2, 1) \).

Si permutamos dos ecuaciones de un sistema \( S_1 \), el nuevo sistema \( S_2 \) es equivalente.

Ejemplo:
Permutamos la primera con la tercera ecuación del sistema \( S_1 \): \[ \left\{ \begin{array}{rcl} 4x + 2y – z &=& 0 \\ -6x – 2y + 2z &=& 4 \\ x + y + 2z &=& -2 \end{array} \right. \Rightarrow \left\{ \begin{array}{rcl} x + y + 2z &=& -2 \\ -6x – 2y + 2z &=& 4 \\ 4x + 2y – z &=& 0 \end{array} \right. \]

Este nuevo sistema es equivalente a \( S_1 \), y ambos tienen como única solución la terna \( (1, 0, -1) \).

Lección 1.1: ¿Qué es una matriz?

Las matrices son una forma organizada de representar datos numéricos en forma de tabla, formada por filas y columnas. Son utilizadas en múltiples áreas del conocimiento para facilitar el análisis de fenómenos que involucran muchas variables.

Origen histórico

El uso de matrices tiene registros antiguos. En un texto matemático chino, escrito alrededor del 250 a.C., ya se utilizaban tablas similares a las matrices para resolver sistemas de ecuaciones.

Definición de matriz

Una matriz del tipo \( m \times n \) (se lee “m por n”) es una tabla ordenada de números, organizada en \( m \) filas y \( n \) columnas. Los elementos de la matriz se representan como \( a_{ij} \), donde \( i \) indica la fila y \( j \) la columna.

Ejemplo: una matriz de tipo \( 3 \times 2 \):

\[ \begin{bmatrix} 6 & 7 \\ 24 & 0 \\ 2 & 21 \end{bmatrix} \]

El elemento que está en la fila 1, columna 1 es \( a_{11} = 6 \).

Aplicaciones

Las matrices se usan para representar datos como producción industrial, estadísticas, modelos económicos, gráficos por computadora, entre otros.

Ejercicio práctico

Una encuesta mostró la expectativa de vida (en años) en diferentes regiones y géneros en Brasil, 2008:

	Norte	Nordeste	Sudeste	Sul	Centro-Oeste
Hombres	69.1	66.5	70.4	71.6	70.6
Mujeres	74.9	73.8	78.5	78.5	77.5

Pregunta: ¿Cuál era la expectativa de vida de una mujer (género 2) en la región Sul (región 4)?

Lección 1.2: Representación y tipos de matrices

Representación genérica

Una matriz se representa de forma general como \( A = (a_{ij})_{m \times n} \), donde:

\( m \): número de filas
\( n \): número de columnas
\( a_{ij} \): elemento ubicado en la fila \( i \) y columna \( j \)

Por ejemplo, la siguiente matriz es de tipo \( 3 \times 2 \):

\[ \begin{bmatrix} 6 & 7 \\ 24 & 0 \\ 2 & 21 \end{bmatrix} \]

Los elementos se indican con dos subíndices: el primero corresponde a la fila, el segundo a la columna.

Ejemplos: \( a_{11} = 6 \), \( a_{21} = 24 \), \( a_{32} = 21 \).

Tipos de matrices

Matriz fila: tiene una sola fila.
Matriz columna: tiene una sola columna.
Matriz cuadrada: tiene el mismo número de filas y columnas.
Matriz nula: todos sus elementos son cero.
Matriz identidad: matriz cuadrada con 1 en la diagonal principal y 0 en las demás posiciones.

Ejemplos

Matriz fila:

\[ \begin{bmatrix} 4 & 5 & 6 \end{bmatrix} \quad (1 \times 3) \]

Matriz columna:

\[ \begin{bmatrix} 3 \\ 1 \\ 2 \end{bmatrix} \quad (3 \times 1) \]

Matriz cuadrada:

\[ \begin{bmatrix} 2 & 0 & 1 \\ -1 & 3 & 4 \\ 0 & 2 & 5 \end{bmatrix} \quad (3 \times 3) \]

Matriz nula:

\[ \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} \]

Matriz identidad de orden 3:

\[ I_3 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \]

Actividad

Indica el tipo y dimensiones de las siguientes matrices:

1. \[ \begin{bmatrix} 3 & 5 & 1 \end{bmatrix} \] 2. \[ \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} \] 3. \[ \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} \]

Lección 1.3: Matrices especiales

En esta lección conocerás tres tipos de matrices muy comunes en matemáticas: la matriz identidad, la matriz nula y la matriz transpuesta.

1. Matriz identidad

Una matriz identidad es una matriz cuadrada en la que todos los elementos de la diagonal principal son iguales a 1 y los demás son 0. Se representa como \( I_n \), donde \( n \) es el orden.

Ejemplos:

\[ I_3 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \quad I_2 = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \quad I_1 = [1] \]

2. Matriz nula

Una matriz nula es aquella en la que todos sus elementos son cero.

Ejemplos:

\[ \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} \quad \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} \quad [0] \]

3. Transpuesta de una matriz

La transpuesta de una matriz \( A \) se representa como \( A^t \) y se obtiene al intercambiar sus filas por columnas.

Ejemplo:

Si \[ A = \begin{bmatrix} 5 & 6 & 0 \\ 24 & 2 & 7 \end{bmatrix} \quad \Rightarrow \quad A^t = \begin{bmatrix} 5 & 24 \\ 6 & 2 \\ 0 & 7 \end{bmatrix} \]

Propiedad: La transpuesta de una matriz \( m \times n \) es una matriz de tipo \( n \times m \).

Actividad

Encuentra la transpuesta de la matriz: \[ B = \begin{bmatrix} 2 & 0 & -5 & 8 \end{bmatrix} \]
Escribe la matriz identidad de orden 4.
Escribe una matriz nula de orden \( 3 \times 3 \).

Lección 1.3: Matrices especiales

En esta lección conocerás tres tipos de matrices muy comunes en matemáticas: la matriz identidad, la matriz nula y la matriz transpuesta.

1. Matriz identidad

Una matriz identidad es una matriz cuadrada en la que todos los elementos de la diagonal principal son iguales a 1 y los demás son 0. Se representa como \( I_n \), donde \( n \) es el orden.

Ejemplos:

\[ I_3 = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right) \quad I_2 = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) \quad I_1 = \left(1\right) \]

2. Matriz nula

Una matriz nula es aquella en la que todos sus elementos son cero.

Ejemplos:

\[ \left( \begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array} \right) \quad \left( \begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right) \quad \left(0\right) \]

3. Transpuesta de una matriz

La transpuesta de una matriz \( A \) se representa como \( A^t \) y se obtiene al intercambiar sus filas por columnas.

Ejemplo:

Si \[ A = \left( \begin{array}{ccc} 5 & 6 & 0 \\ 24 & 2 & 7 \end{array} \right) \quad \Rightarrow \quad A^t = \left( \begin{array}{cc} 5 & 24 \\ 6 & 2 \\ 0 & 7 \end{array} \right) \]

Propiedad: La transpuesta de una matriz \( m \times n \) es una matriz de tipo \( n \times m \).

Actividad

Encuentra la transpuesta de la matriz: \[ B = \left( \begin{array}{cccc} 2 & 0 & -5 & 8 \end{array} \right) \]
Escribe la matriz identidad de orden 4.
Escribe una matriz nula de orden \( 3 \times 3 \).

Ejemplos Ecuaciones Matriciales

Ejemplos:

Despejar la matriz \( X \) en las siguientes ecuaciones matriciales:

① \( X + A = B \)
\( \Rightarrow X = B – A \)

② \( X – A = B \)
\( \Rightarrow X = B + A \)

③ \( 3X + A = B \)
\( \Rightarrow 3X = B – A \Rightarrow X = \frac{1}{3}(B – A) \)

④ \( A \cdot X = B \)
\( \color{red}{A^{-1}} \cdot A \cdot X = \color{red}{A^{-1}} \cdot B \Rightarrow \color{green}{I} \cdot X = A^{-1} \cdot B \Rightarrow X = A^{-1} \cdot B \)

⑤ \( X \cdot A = B \)
\( X \cdot A \cdot \color{red}{A^{-1}} = B \cdot \color{red}{A^{-1}} \Rightarrow X \cdot \color{green}{I} = B \cdot A^{-1} \Rightarrow X = B \cdot A^{-1} \)

Ejemplos Ecuaciones Matriciales

Ejemplos:

Despejar la matriz \( X \) en las siguientes ecuaciones matriciales:

① \( X + A = B \)
\( \Rightarrow X = B – A \)

② \( X – A = B \)
\( \Rightarrow X = B + A \)

③ \( 3X + A = B \)
\( \Rightarrow 3X = B – A \Rightarrow X = \frac{1}{3}(B – A) \)

④ \( A \cdot X = B \)
\[ \underbrace{A^{-1} \cdot A}_{I} \cdot X = A^{-1} \cdot B \Rightarrow I \cdot X = A^{-1} \cdot B \Rightarrow X = A^{-1} \cdot B \]

⑤ \( X \cdot A = B \)
\[ X \cdot \underbrace{A \cdot A^{-1}}_{I} = B \cdot A^{-1} \Rightarrow X \cdot I = B \cdot A^{-1} \Rightarrow X = B \cdot A^{-1} \]

Ejemplos Ecuaciones Matriciales

Ejemplos:

Despejar la matriz \( X \) en las siguientes ecuaciones matriciales:

① \( X + A = B \)

Resta la matriz \( A \) en ambos lados de la ecuación:
\[ X = B – A \]

② \( X – A = B \)

Suma la matriz \( A \) en ambos lados de la ecuación:
\[ X = B + A \]

③ \( 3X + A = B \)

Resta la matriz \( A \): \( 3X = B – A \)
Luego divide entre 3 (escalar):
\[ X = \frac{1}{3}(B – A) \]

④ \( A \cdot X = B \)

Multiplica por la inversa de \( A \) a la izquierda:
\[ \underbrace{A^{-1} \cdot A}_{I} \cdot X = A^{-1} \cdot B \] Como \( A^{-1} \cdot A = I \), queda:
\[ I \cdot X = A^{-1} \cdot B \Rightarrow X = A^{-1} \cdot B \]

⑤ \( X \cdot A = B \)

Multiplica por la inversa de \( A \) a la derecha:
\[ X \cdot \underbrace{A \cdot A^{-1}}_{I} = B \cdot A^{-1} \] Como \( A \cdot A^{-1} = I \), queda:
\[ X \cdot I = B \cdot A^{-1} \Rightarrow X = B \cdot A^{-1} \]

AX – X A = B \[ \begin{pmatrix} 1 & 2 \\ -1 & 3 \end{pmatrix} \cdot \begin{pmatrix} x & 0 \\ y & z \end{pmatrix} – \begin{pmatrix} x & 0 \\ y & z \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\ -1 & 3 \end{pmatrix} = \begin{pmatrix} 2 & -6 \\ -1 & -2 \end{pmatrix} \] => \[ \begin{pmatrix} x + 2y & 2z \\ -x + 3y & 3z \end{pmatrix} – \begin{pmatrix} x & 2x \\ y – z & 2y + 3z \end{pmatrix} = \begin{pmatrix} 2 & -6 \\ -1 & 2 \end{pmatrix} = D \] => \[ \begin{pmatrix} 2y & 2z – 2x \\ -x + 2y + z & -2y \end{pmatrix} = \begin{pmatrix} 2 & -6 \\ -1 & -2 \end{pmatrix} \] => \[ \begin{pmatrix} 2y & 2z – 2x \\ -x + 2y + z & -2y \end{pmatrix} = \begin{pmatrix} 2 & -6 \\ -1 & -2 \end{pmatrix} \] \[ 2y = 2 \quad y = 1 \] \[ 2z – 2x = -6 \quad x = 3 + 2 \] \[ -x + 2y + z = -1 \quad x = 3 + 2 \] \[ -2y = -2 \quad y = 1 \] \[ x = \begin{pmatrix} 3 + z & 0 \\ 1 & 2 \end{pmatrix} \forall z \in \mathbb{R} \]

Resolución de Ecuación Matricial AX – XA = B

Problema:

Resolver la ecuación matricial:

AX – XA = B

Donde:

A = \[ \begin{pmatrix} 1 & 2 \\ -1 & 3 \end{pmatrix} \]

X = \[ \begin{pmatrix} x & 0 \\ y & z \end{pmatrix} \]

B = \[ \begin{pmatrix} 2 & -6 \\ -1 & -2 \end{pmatrix} \]

Paso 1: Desarrollar AX y XA

Calculamos primero AX:

\[ AX = \begin{pmatrix} 1 & 2 \\ -1 & 3 \end{pmatrix} \begin{pmatrix} x & 0 \\ y & z \end{pmatrix} = \begin{pmatrix} \color{red}{x + 2y} & \color{blue}{2z} \\ \color{green}{-x + 3y} & \color{purple}{3z} \end{pmatrix} \]

Luego calculamos XA:

\[ XA = \begin{pmatrix} x & 0 \\ y & z \end{pmatrix} \begin{pmatrix} 1 & 2 \\ -1 & 3 \end{pmatrix} = \begin{pmatrix} \color{red}{x} & \color{blue}{2x} \\ \color{green}{y – z} & \color{purple}{2y + 3z} \end{pmatrix} \]

Paso 2: Realizar la resta AX – XA

\[ AX – XA = \begin{pmatrix} x+2y & 2z \\ -x+3y & 3z \end{pmatrix} – \begin{pmatrix} x & 2x \\ y-z & 2y+3z \end{pmatrix} = \begin{pmatrix} \color{red}{2y} & \color{blue}{2z-2x} \\ \color{green}{-x+2y+z} & \color{purple}{-2y} \end{pmatrix} \]

Igualamos a B:

\[ \begin{pmatrix} 2y & 2z-2x \\ -x+2y+z & -2y \end{pmatrix} = \begin{pmatrix} 2 & -6 \\ -1 & -2 \end{pmatrix} \]

Paso 3: Resolver el sistema de ecuaciones

Igualando componente a componente:

\[ \color{red}{2y = 2} \] \[ \Rightarrow y = 1 \]

\[ \color{blue}{2z – 2x = -6} \] \[ \Rightarrow x = z + 3 \]

\[ \color{green}{-x + 2y + z = -1} \] \[ \Rightarrow -x + z = -3 \]

\[ \color{purple}{-2y = -2} \] \[ \Rightarrow y = 1 \]

Sustituyendo y resolviendo:

De la primera ecuación: y = 1

Sustituyendo x = z + 3 en -x + z = -3:

-(z + 3) + z = -3 → -3 = -3 (se cumple ∀z ∈ ℝ)

Por tanto, la solución es:

\[ x = z + 3 \] \[ y = 1 \] \[ z \text{ es libre} \]

Solución Final:

\[ X = \begin{pmatrix} z + 3 & 0 \\ 1 & z \end{pmatrix} \quad \forall z \in \mathbb{R} \]

La solución depende de un parámetro libre z, lo que indica que hay infinitas soluciones.

1Planteamiento del Problema

Resolver la ecuación matricial:

AX – XA = B

Matriz A

\[ A = \begin{pmatrix} 1 & 2 \\ -1 & 3 \end{pmatrix} \]

Matriz X (incógnita)

\[ X = \begin{pmatrix} x & 0 \\ y & z \end{pmatrix} \]

Matriz B

\[ B = \begin{pmatrix} 2 & -6 \\ -1 & -2 \end{pmatrix} \]

2Desarrollo de AX y XA

Cálculo de AX:

Cálculo de XA:

3Realizar la resta AX – XA

Igualando a la matriz B:

\[ \begin{pmatrix} 2y & 2z-2x \\ -x+2y+z & -2y \end{pmatrix} = \begin{pmatrix} 2 & -6 \\ -1 & -2 \end{pmatrix} \]

4Sistema de Ecuaciones Resultante

\[ \color{red}{2y = 2} \]

Solución: \( y = 1 \)

\[ \color{blue}{2z – 2x = -6} \]

Simplificando: \( x = z + 3 \)

\[ \color{green}{-x + 2y + z = -1} \]

Sustituyendo: \( -x + z = -3 \)

\[ \color{purple}{-2y = -2} \]

Confirmación: \( y = 1 \)

Resolución del sistema:

De \( y = 1 \) y \( x = z + 3 \), sustituyendo en la tercera ecuación:

\( -(z + 3) + z = -3 \) → \( -3 = -3 \) (se cumple para todo \( z \in \mathbb{R} \))

Por tanto, \( z \) es un parámetro libre.

Solución General

\[ X = \begin{pmatrix} z + 3 & 0 \\ 1 & z \end{pmatrix} \quad \text{para cualquier } z \in \mathbb{R} \]

El sistema tiene infinitas soluciones dependiendo del valor del parámetro libre z.

Matriz Triangular Superior

✶ Matriz Triangular Superior:

Es una matriz cuadrada en la cual los elementos \( a_{ij} \) son nulos cuando se cumple que \( i > j \).

\[ A = \begin{pmatrix} \color{red}{1} & 2 & 3 \\ 0 & \color{red}{4} & 5 \\ 0 & 0 & \color{red}{6} \end{pmatrix} \]

En la matriz triangular superior son nulos los elementos que quedan debajo de la diagonal principal.

Matriz Triangular Superior:
Es la matriz cuadrada que tiene nulos los elementos a_ij que verifican i > j

\[ A = \begin{pmatrix} 1 & 2 & 3 \\ 0 & 4 & 5 \\ 0 & 0 & 6 \end{pmatrix} \]

En la matriz triangular superior son nulos los elementos que quedan DEBAJO de la diagonal.

Matriz Triangular Superior

Es la matriz cuadrada que tiene nulos los elementos a_ij que verifican i > j

\[ A = \begin{pmatrix} 1 & 2 & 3 \\ 0 & 4 & 5 \\ 0 & 0 & 6 \end{pmatrix} \]

Matriz Triangular Superior

Una matriz triangular superior es una matriz cuadrada en la cual todos los elementos por debajo de la diagonal principal son nulos. Formalmente, una matriz \( A = [a_{ij}] \) es triangular superior si \( a_{ij} = 0 \) para todo \( i > j \).

\[ A = \begin{pmatrix} \class{diagonal-element}{1} & 2 & 3 \\ 0 & \class{diagonal-element}{4} & 5 \\ 0 & 0 & \class{diagonal-element}{6} \end{pmatrix} \]

Los elementos debajo de la diagonal principal (mostrados como ceros) son nulos, mientras que los elementos sobre la diagonal (incluyendo los elementos diagonales en rojo) pueden tener cualquier valor.

La diagonal principal está formada por los elementos donde \( i = j \).

Matriz Triangular Inferior

Una matriz triangular inferior es una matriz cuadrada en la cual todos los elementos por encima de la diagonal principal son nulos. Formalmente, una matriz \( A = [a_{ij}] \) es triangular inferior si \( a_{ij} = 0 \) para todo \( i < j \).

\[ A = \begin{pmatrix} \class{diagonal-element}{1} & 0 & 0 \\ 2 & \class{diagonal-element}{4} & 0 \\ 3 & 5 & \class{diagonal-element}{6} \end{pmatrix} \]

Los elementos encima de la diagonal principal (mostrados como ceros) son nulos, mientras que los elementos bajo la diagonal (incluyendo los elementos diagonales en rojo) pueden tener cualquier valor.

La diagonal principal sigue siendo la formada por los elementos donde \( i = j \).

Matriz Diagonal

Matriz Fila

Una matriz fila es una matriz que consta de una sola fila y múltiples columnas. Formalmente, es una matriz de dimensión \( 1 \times n \) que puede representarse como \( A = [a_{1j}] \) donde \( j = 1, 2, \ldots, n \).

Ejemplo 1: Vector fila simple

\[ A = \begin{pmatrix} 3 & 1 & 4 & 2 \end{pmatrix} \]

Matriz fila con 4 elementos (dimensión \( 1 \times 4 \))

Ejemplo 2: Coeficientes polinomiales

\[ B = \begin{pmatrix} 1 & -5 & 6 & -2 \end{pmatrix} \]

Representa los coeficientes del polinomio \( x^3 – 5x^2 + 6x – 2 \)

Ejemplo 3: Probabilidades

\[ C = \begin{pmatrix} 0.2 & 0.3 & 0.5 \end{pmatrix} \]

Distribución de probabilidades (suma = 1)

Las matrices fila son fundamentales en álgebra lineal y tienen aplicaciones en:

Representación de vectores en espacios vectoriales
Sistemas de ecuaciones lineales
Modelos de probabilidad y estadística
Coeficientes de polinomios

La transpuesta de una matriz fila es una matriz columna, y viceversa.

Introducción a las Matrices

Las matrices son una herramienta fundamental en matemáticas que permiten organizar y manipular datos de manera estructurada. Históricamente, su estudio comenzó en el siglo XIX con contribuciones de matemáticos como William Rowan Hamilton, Hermann Günther Grassmann y Arthur Cayley, quienes desarrollaron un tipo de álgebra matricial que abrió las puertas al campo del álgebra abstracta.

Definición formal:

Una matriz de orden m × n (con m, n ∈ ℕ*) es todo cuadro rectangular con m·n elementos, dispuestos en m filas y n columnas.

\[ A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} \]

Donde cada elemento a_ij se ubica en la intersección de la i-ésima fila con la j-ésima coluna.

Ejemplo práctico:

Consideremos los gastos diarios de Isabela durante 3 días:

\[ \begin{bmatrix} 6,00 & 8,70 & 2,00 & 2,50 \\ 6,00 & 14,00 & 5,30 & 0 \\ 6,00 & 12,90 & 0 & 4,00 \end{bmatrix} \]

Esta matriz 3×4 muestra:

Cada fila representa un día diferente
Cada columna representa un tipo de gasto (transporte, comida, café, dulces)
El elemento a₃₂ = 12,90 representa lo gastado el miércoles en comida

Introducción a las Matrices

Definición formal:

Una matriz de orden m × n (con m, n ∈ ℕ*) es todo cuadro rectangular con m·n elementos, dispuestos en m filas y n columnas.

\[ A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} \]

Los elementos se denotan como a_ij, donde i indica la fila y j la columna. La matriz se puede indicar abreviadamente como A = (a_ij)_m×n.

Ejemplo 1: Matriz 2×3

\[ \begin{pmatrix} 1 & -6 & 0 \\ 0 & 1 & -7 \end{pmatrix} \]

Matriz con 2 filas y 3 columnas. El elemento a₂₃ = -7.

Ejemplo 2: Matriz 1×5

\[ \begin{pmatrix} 0 & 3 & -8 & 6 & -17 \end{pmatrix} \]

Matriz fila con 5 elementos. El elemento a₁₄ = 6.

Ejemplo 3: Matriz 3×3

\[ \begin{pmatrix} 1 & 0 & 3 \\ 1 & -2 & \sqrt{2} \\ 0 & -5 & 4 \end{pmatrix} \]

Matriz cuadrada (mismo número de filas y columnas). El elemento a₃₂ = -5.

Ejemplo 4: Matriz 4×2

\[ \begin{pmatrix} 3 & 6 \\ 0 & 2 \\ -7 & 0 \\ -2 & 9 \end{pmatrix} \]

Matriz con 4 filas y 2 columnas. El elemento a₄₁ = -2.

Notación y elementos

Para la matriz A = \[ \begin{bmatrix} 3 & -5 \\ 7 & 10 \end{bmatrix} \]

a₁₁ = 3 (1ª fila, 1ª columna)
a₁₂ = -5 (1ª fila, 2ª coluna)
a₂₁ = 7 (2ª fila, 1ª columna)
a₂₂ = 10 (2ª fila, 2ª columna)

La lista ordenada (a₁₁, a₁₂, …, a_1n) se llama la i-ésima fila de la matriz, mientras que (a_1j, a_2j, …, a_mj) es la j-ésima columna.

Introducción a las Matrices

Definición formal:

Una matriz de orden m × n (con m, n ∈ ℕ*) es todo cuadro rectangular con m·n elementos, dispuestos en m filas y n columnas.

\[ A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} \]

Los elementos se denotan como a_ij, donde i indica la fila y j la columna. La matriz se puede indicar abreviadamente como A = (a_ij)_m×n.

Ejemplo 1: Matriz 3×4

\[ \begin{pmatrix} 5 & 8 & -1 & 0 \\ 2 & 4 & 7 & -3 \\ 9 & 0 & 2 & 6 \end{pmatrix} \]

Matriz con 3 filas y 4 columnas. El elemento a₂₃ = 7.

Ejemplo 2: Matriz 1×6

\[ \begin{pmatrix} 2 & -4 & 7 & 0 & 9 & -5 \end{pmatrix} \]

Matriz fila con 6 elementos. El elemento a₁₅ = 9.

Ejemplo 3: Matriz 4×4

\[ \begin{pmatrix} 3 & 0 & -2 & 5 \\ 1 & 4 & 0 & 8 \\ 7 & 2 & 6 & -1 \\ 0 & 9 & 3 & 4 \end{pmatrix} \]

Matriz cuadrada (mismo número de filas y columnas). El elemento a₄₂ = 9.

Ejemplo 4: Matriz 5×2

\[ \begin{pmatrix} 1 & 6 \\ 0 & 3 \\ -4 & 0 \\ 2 & 8 \\ -5 & 7 \end{pmatrix} \]

Matriz con 5 filas y 2 columnas. El elemento a₅₁ = -5.

Notación y elementos

Para la matriz A = \[ \begin{bmatrix} 4 & -2 \\ 9 & 5 \end{bmatrix} \]

a₁₁ = 4 (1ª fila, 1ª columna)
a₁₂ = -2 (1ª fila, 2ª coluna)
a₂₁ = 9 (2ª fila, 1ª columna)
a₂₂ = 5 (2ª fila, 2ª columna)

La lista ordenada (a₁₁, a₁₂, …, a_1n) se llama la i-ésima fila de la matriz, mientras que (a_1j, a_2j, …, a_mj) es la j-ésima columna.

Matriz Fila

✶ Matriz Fila:

Una matriz fila es una matriz que tiene una sola fila y una o más columnas. Es decir, su dimensión es \( 1 \times n \).

\( A_{1 \times 3} \)

\[ A = \begin{pmatrix} 2 & 5 & -1 \end{pmatrix} \]

\( B_{1 \times 4} \)

\[ B = \begin{pmatrix} 7 & 0 & 3 & 8 \end{pmatrix} \]

\( C_{1 \times 2} \)

\[ C = \begin{pmatrix} -4 & 6 \end{pmatrix} \]

En una matriz fila, todos los elementos están dispuestos horizontalmente en una sola fila.

Matriz Columna

✶ Matriz Columna:

Una matriz columna es una matriz que tiene una sola columna y una o más filas. Es decir, su dimensión es \( m \times 1 \).

\( A_{3 \times 1} \)

\[ A = \begin{pmatrix} 4 \\ -2 \\ 7 \end{pmatrix} \]

\( B_{2 \times 1} \)

\[ B = \begin{pmatrix} 0 \\ 5 \end{pmatrix} \]

\( C_{4 \times 1} \)

\[ C = \begin{pmatrix} 9 \\ 1 \\ -3 \\ 6 \end{pmatrix} \]

En una matriz columna, todos los elementos están organizados verticalmente en una sola columna.

Matriz Cuadrada

✶ Matriz Cuadrada:

Una matriz cuadrada es aquella que tiene el mismo número de filas y columnas. Su dimensión es \( n \times n \).

\( A_{2 \times 2} \)

\[ A = \begin{pmatrix} 1 & -3 \\ 4 & 0 \end{pmatrix} \]

\( B_{3 \times 3} \)

\[ B = \begin{pmatrix} 5 & 0 & 2 \\ -1 & 3 & 4 \\ 7 & 8 & 6 \end{pmatrix} \]

\( C_{4 \times 4} \)

\[ C = \begin{pmatrix} 2 & 1 & 0 & -3 \\ 0 & 5 & 7 & 2 \\ 4 & 0 & 6 & 1 \\ 9 & 8 & 3 & 0 \end{pmatrix} \]

Las matrices cuadradas tienen propiedades especiales, como la posibilidad de calcular determinantes e inversas si son regulares.

Matriz Fila

Una matriz fila tiene una sola fila y varias columnas. Su dimensión es \( 1 \times n \).

\( A_{1 \times 3} \)

\[ A = \begin{pmatrix} 2 & 5 & -1 \end{pmatrix} \]

\( B_{1 \times 4} \)

\[ B = \begin{pmatrix} 7 & 0 & 3 & 8 \end{pmatrix} \]

\( C_{1 \times 2} \)

\[ C = \begin{pmatrix} -4 & 6 \end{pmatrix} \]

… igual head …

Matriz Columna

Una matriz columna tiene una sola columna y varias filas. Su dimensión es \( m \times 1 \).

\( A_{3 \times 1} \)

\[ A = \begin{pmatrix} 4 \\\\ -2 \\\\ 7 \end{pmatrix} \]

\( B_{2 \times 1} \)

\[ B = \begin{pmatrix} 0 \\\\ 5 \end{pmatrix} \]

\( C_{4 \times 1} \)

\[ C = \begin{pmatrix} 9 \\\\ 1 \\\\ -3 \\\\ 6 \end{pmatrix} \]

… igual head …

Matriz Cuadrada

Una matriz cuadrada tiene el mismo número de filas y columnas. Su dimensión es \( n \times n \).

\( A_{2 \times 2} \)

\[ A = \begin{pmatrix} 1 & -3 \\\\ 4 & 0 \end{pmatrix} \]

\( B_{3 \times 3} \)

\[ B = \begin{pmatrix} 5 & 0 & 2 \\\\ -1 & 3 & 4 \\\\ 7 & 8 & 6 \end{pmatrix} \]

\( C_{4 \times 4} \)

\[ C = \begin{pmatrix} 2 & 1 & 0 & -3 \\\\ 0 & 5 & 7 & 2 \\\\ 4 & 0 & 6 & 1 \\\\ 9 & 8 & 3 & 0 \end{pmatrix} \]

… igual head …

Matriz Nula

Una matriz nula es aquella en la que todos sus elementos son cero. Se denota como \( 0 \).

\( A_{2 \times 3} \)

\[ A = \begin{pmatrix} 0 & 0 & 0 \\\\ 0 & 0 & 0 \end{pmatrix} \]

\( B_{1 \times 4} \)

\[ B = \begin{pmatrix} 0 & 0 & 0 & 0 \end{pmatrix} \]

\( C_{3 \times 3} \)

\[ C = \begin{pmatrix} 0 & 0 & 0 \\\\ 0 & 0 & 0 \\\\ 0 & 0 & 0 \end{pmatrix} \]

… igual head …

Matriz Identidad

La matriz identidad es una matriz cuadrada con unos en la diagonal principal y ceros en el resto. Se denota por \( I \).

\( A = I_2 \)

\[ A = \begin{pmatrix} 1 & 0 \\\\ 0 & 1 \end{pmatrix} \]

\( B = I_3 \)

\[ B = \begin{pmatrix} 1 & 0 & 0 \\\\ 0 & 1 & 0 \\\\ 0 & 0 & 1 \end{pmatrix} \]

\( C = I_4 \)

\[ C = \begin{pmatrix} 1 & 0 & 0 & 0 \\\\ 0 & 1 & 0 & 0 \\\\ 0 & 0 & 1 & 0 \\\\ 0 & 0 & 0 & 1 \end{pmatrix} \]

Matriz Fila

Una matriz fila tiene una sola fila y varias columnas. Su dimensión es \( 1 \times n \).

\( A_{1 \times 3} \)

\[ A = \begin{pmatrix} 2 & 5 & -1 \end{pmatrix} \]

\( B_{1 \times 4} \)

\[ B = \begin{pmatrix} 7 & 0 & 3 & 8 \end{pmatrix} \]

\( C_{1 \times 2} \)

\[ C = \begin{pmatrix} -4 & 6 \end{pmatrix} \]